Conditional Random Field

In this post, I briefly explain what is conditional random Fields and how they can be used for sequence labeling. CRF is a discriminative model best suited for tasks in which contextual information or state of the neighbors affects the current prediction. CRFs are widely used in named entity recognition, part of speech tagging, gene prediction, noise reduction, and object detection problems.

In order to understand this post, it’s helpful to first read about Hidden Markov Models and Gibbs Distribution. This video explains the basics of HMM and this video by Daphne Koller is a very good introduction on Gibbs distribution.

Now let’ see why we need CRF?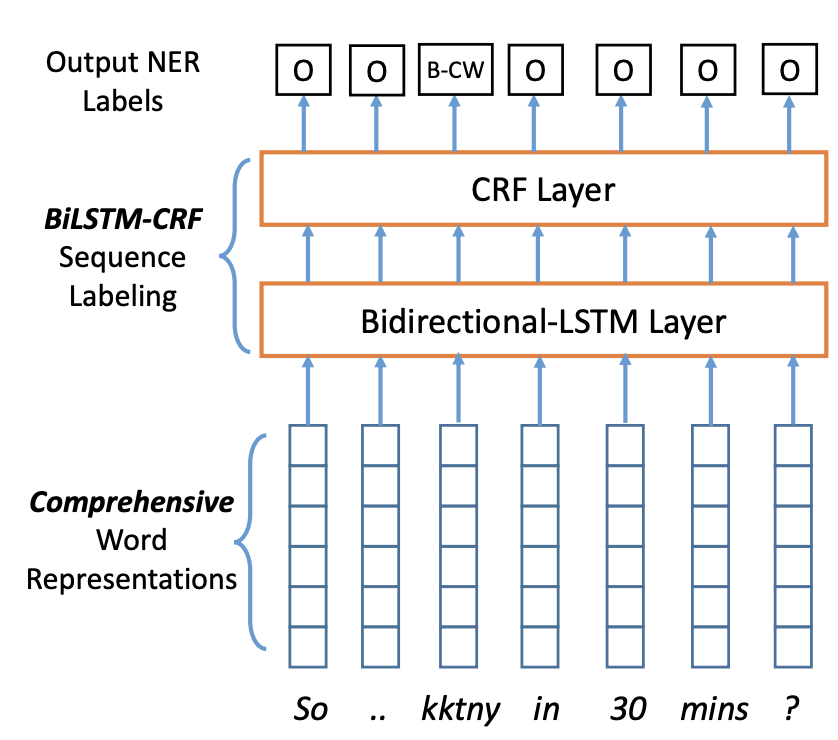

From the paper

NER is in general formulated as a sequence labeling problem with a multi-layer Perceptron + Softmax layer as the tag decoder layer. The architecture can be a bidirectional LSTM with a softmax layer on top. The softmax layer predicts the tag for each token (e.g. B-PER, I_LOC). One shortcoming of using the softmax layer on top is that each token is predicted indepently. So it is possible that the sequence of tags is incosistent, for exaple, B_PER, I_LOC, O, O, I_PER.

In order to overcome this shortcoming, instead of using a softmax layer, we can use a Conditional Random Field (CRF) layer on top. When CRF is predicting the tag for a sequence, it also considers the surronding tokens and their tags into account as well. More formally, a Conditional Random Field* (CRF) is a standard model for predicting the most likely sequence of labels that correspond to a sequence of inputs.

Formally, we can take the above sequence of hidden states h = (h1, h2, …, hn) as our input to the CRF layer, and its output is our final prediction label sequence y = (y1, y2, …, yn), where yi in the set of all possible labels. We denote Y(h) as the set of all possible label sequences. Then we can derive the conditional probability of the output sequence given the input hidden state sequence is

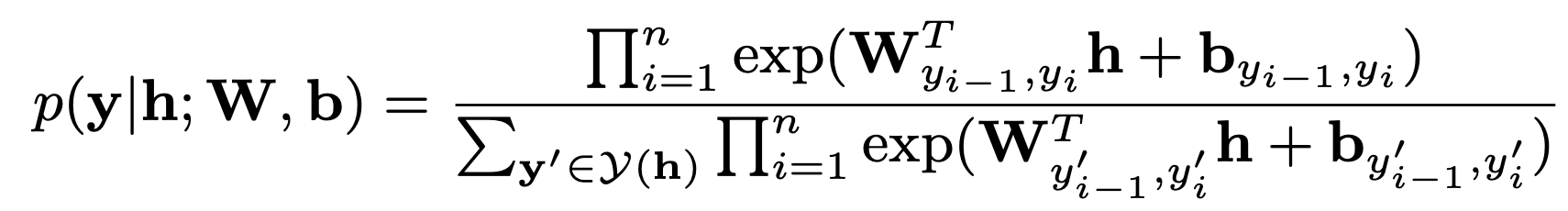
where W and b are the two weight matrices and the subscription indicates that we extract the weight vector for the given label pair (yi−1, yi). To train the CRF layer, we can use the classic maximum conditional likelihood estimation to train our model. The final log-likelihood with respect to the weight matrices is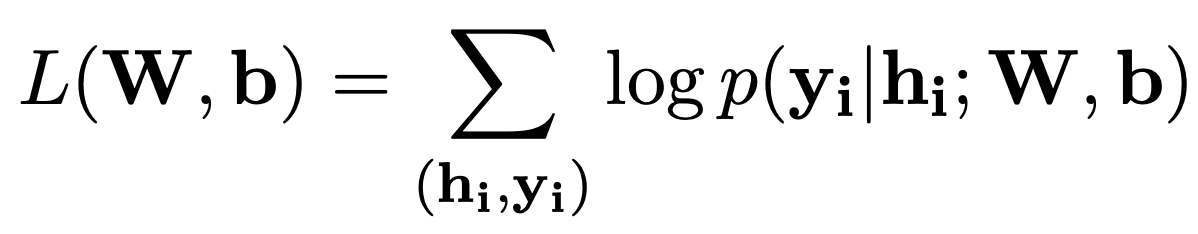

Finally, we can adopt the Viterbi algorithm for training the CRF layer and the decoding the optimal output sequence y.

For a very nice explanation of CRF, I highly recommend watching these videos by Hugo Larochelle