Knowledge Distillation

In this post, I will discuss what is knowledge distillation (also refered as Student-Teacher Learning), what is the intuition behind it, and why it works!

Paper: Distilling the Knowledge in a Neural Network

We have built sophisticated models that solve complex problems such as natural language inference and common sense reasoning. However, these large, high performing models come with their own costs. They need a huge amount of computational resources (such as GPU’s memory), are slow (depending on computation resources), and hence cannot be run on low resource devices such as a mobile device. When computational resources are limited, the model can be made smaller by sharing parameters, quantization, and knowledge distillation. Knowledge distillation is a very successful model compression method in which a small model is trained to mimic a pre-trained, larger mode.

In distillation, a large trained model (teacher) is distilled in a smaller model (student). The important point is that the cost function of the student model is the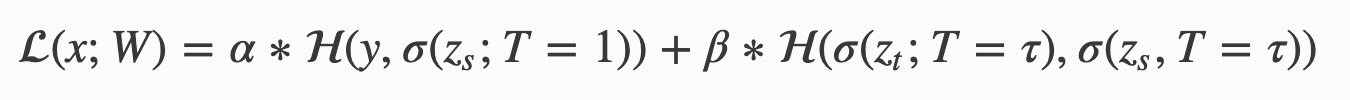

where x is the input, W is the student model parameters, y is the ground truth label, H is the cross-entropy loss function, σ is the softmax function parameterized by the temperature T, and α and β are coefficients. zs and zt are the logits of the student and teacher respectively.

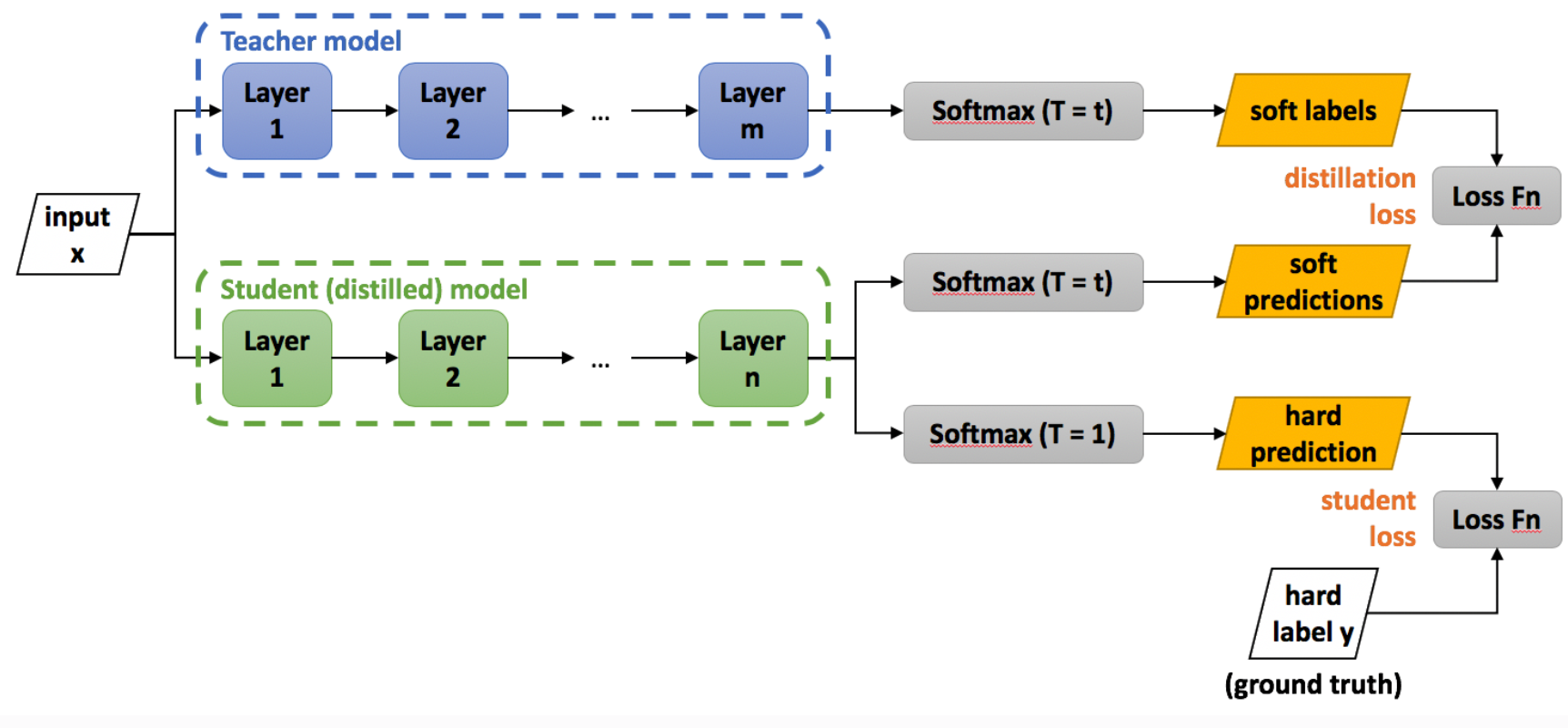
Why distillation works: In my opinion there are two reasons that distillation works really well, transferring (1) dark knowledge and (2) learning winning the lottery ticket

Transferring dark knowledge Remember the cost function of the teacher model: cross-entropy(students’ prediction, ground truth) + cross-entropy(student’s prediction (with temperature cross-entropy), teacher’s prediction (with temperature cross entropy))

The first part is the usual cross-entropy, however, the second part is transferring the dark knowledge from the teacher model to the distilled model. What is dark knowledge? For example, if the model is classifying images, the input is an image and the true label, e.g. A cat. The output of the large model, however, is the distribution of the probabilities of the classes. For the image of a cat as the input, the model gives 0 probability for the image to be a computer, however, the model produces 0.2 probability for the image to be a lion or a dog. Hence, it has much more information (AKA dark knowledge) compared to the input labels. This knowledge is then transferred to the distilled model with the second cross-entropy. Hence, in addition to the available class labels, the student model can use to use soft probabilities (or‘logits’) of the teacher mode. It has the effect of giving much more information for each input data to the model and makes the input to the student’s model much richer.

(2) Learning the winning lottery ticket Often in knowledge distillation, the student model’s intermediate layers are forced to output a result similar to the teacher’s intermediate layers. For example, if the teacher model is 12 layer BERT and the student model is 6 layer BERT, the output of the first layer of the distilled model should look like the output of the 2nd layer of the teacher BERT. Why does this help? Remember the “Lottery Ticket Hypothesis” paper, the main idea of deep learning and very large models is that it tries many representations and embeddings and since it’s trying many many representations, the one that helps the ML task is also embedded in the trained model. Hence, the large/teacher model has all those trial and errors and useful representation. The distilled model is forcing the intermediate representations to look like an intermediate representation of the large model and hence forced to pick up only the useful representations (the winning lottery only) from the larger model.